封闭离散点的边界寻找方法

2020-03-30

在很多情况下我们需要对离散点进行封闭拟合，比如在图像识别领域中的物体轮廓提取，逆向工程中的三维扫描重建等等，完成对目标的轮廓提取或扫描后往往得到的是具有大量的离散点云。本文主要给出基于MATLAB的依据二维和三维中的点构建的多边形和多面体的功能函数总结。

研究现状

由于干扰因素的存在和测量条件的限制，得到的目标边缘散点或表面散点会出现强噪声，边缘断裂，表面孔洞，异常数据点等现象。针对这些现象，许多学者都提出了相应的求解方法，如二维轮廓离散点的局部连接法、最小二乘法曲线拟合、Hough变换、基于视觉感知边缘连接（Visual Perception Edge Linking，VPEL）算法、基于顺序边缘连接（Sequential Edge Linking，SEL）算法以及基于模糊判定的边缘连接方法等；还有三维表面离散点的隐式曲面方法、最小移动二乘法、单元多层次分解方法、(泊松流)曲面重构、变分方法、机器学习／统计学方法等。

其中赵亮等人提出一种由截面上散点生成的最短路径拟合轮廓曲面的方法，通过构造最短截面路径，得到多层截面的轮廓线，从而在相邻的截面间生成轮廓曲面，最后基于曲率流的光顺方法对曲面进行光顺处理，在三维地震体数据可视化的具体应用实验中获得了较好的效果。刘光帅等人提出了一种点云重构算法，通过候选筛分边界点进行拓扑初始化，利用泛洪(flooding)算法进行边界封闭环提取，基于统计学方法对边界进行优化，获得分段光滑的网格曲面。徐毅等人提出一种基于路径形态学的断裂边缘修复技术，通过考虑等照度线曲率、梯度值、边缘端点前进方向等多重判据构建形态学闭算子，对边缘图进行路径闭运算，从而完成对断裂边缘的连接。顾天奇等人提出一种基于移动最小二乘法构造了一种新的封闭离散点拟合方法，基于封闭离散点的几何特征，提出一种新的权值确定方法，该方法通过构造一个与弦长有关的点，赋予支持域内各点的权值，使临近点的权值变化逐步衰减，实现了拟合曲线的局部逼近，在叶片截面形线离散点拟合中取得了很好的效果。

凸包算法

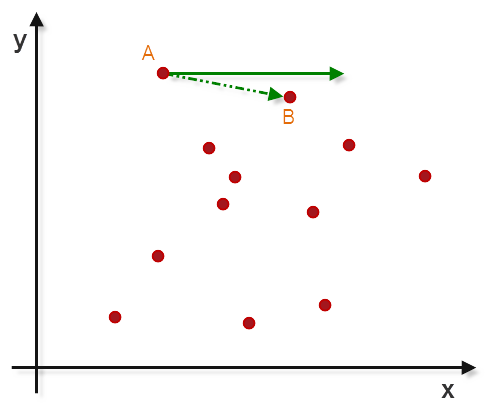
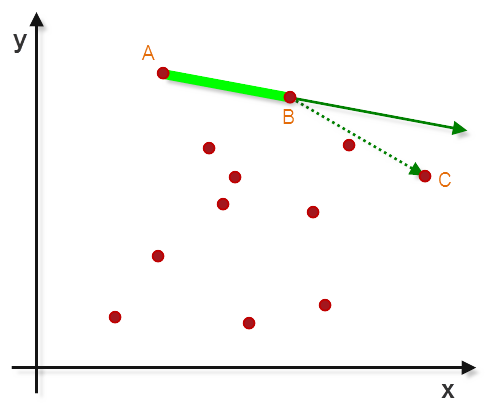
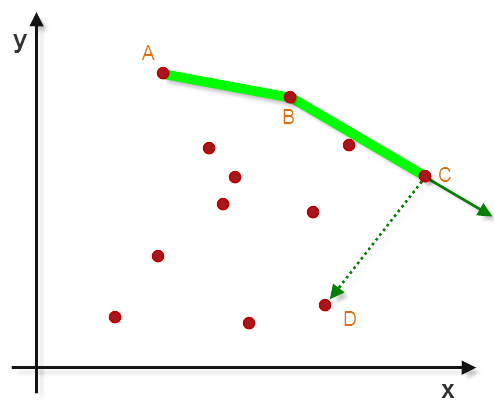
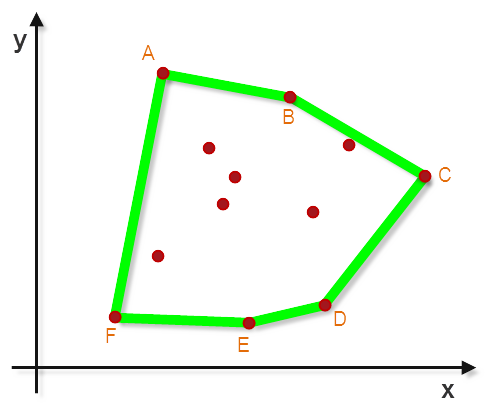
对于二维离散点密度较小的情况下，进行凸多边形勾勒往往可以采用凸包算法，该算法的实现思路如下： 1. 找到离散点中，保证y坐标最大的情况下，x坐标最小的点，记做A点 2. 以A点为原点，x轴正反向射线（Ax）顺时针扫描，找到旋转角最小时扫描到的点，记做B点 3. 以B点为原点，AB方向射线（AB）顺时针扫描，找到旋转角最小时扫描到的点，记做C点 4. 以C点为原点，BC方向射线（BC）顺时针扫描，找到旋转角最小时扫描到的点，记做D点 5. 以此类推，直到找到起始点A

Matlab已将凸包算法集成于convhull这个函数中，其语法如下：

k = convhull(P) %计算矩阵P中点的二维或三维凸包。
k = convhull(x,y) %计算列向量x和y中点的二维凸包。
k = convhull(x,y,z) %计算列向量x、y和z中点的三维凸包。
k = convhull(___,'Simplify',tf) %指定是否删除不影响凸包面积或体积的顶点。默认情况下，tf 为 false。
[k,av] = convhull(___) %也计算凸包的面积或体积。

## Alpha Shapes ##

对于凸包算法往往只能用于勾勒凸多边形，在非凸多边形中往往不能取得预期的结果，比如我需要求下图（a）中的边界，但是用凸包算法得到的是（b）中的结果，我们理想的结果是（c）中得到的边界，这时候就要寻求另一种算法。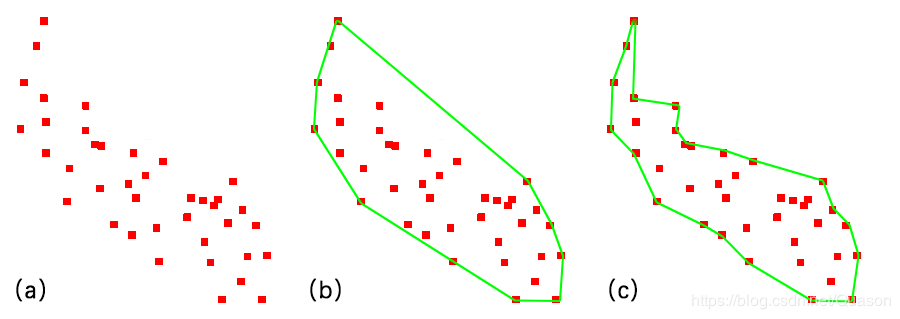

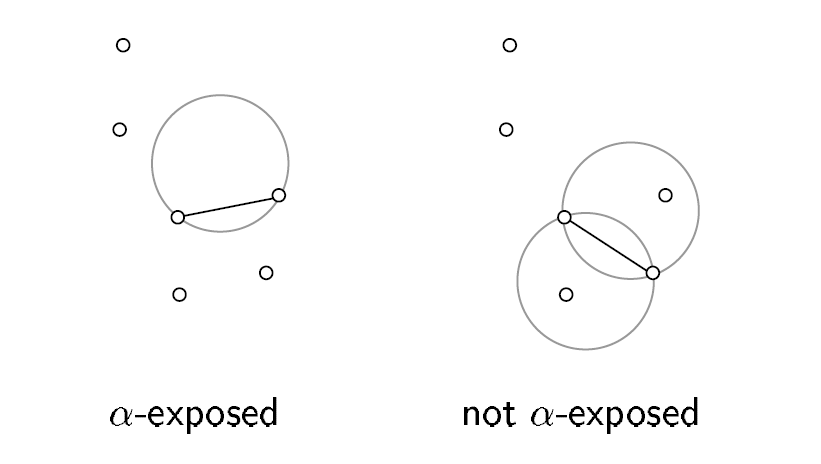
Alpha Shapes可以用来从一堆无序的点集中提取边缘，这个边界不一定是凸的，也不一定是联通的，但是其一定程度上表示了这一组离散点的轮廓。通过调节参数可以使边界更加精细或粗糙。设有一点集S的Alpha-Shapes是一个多边形，这个多边形是由点集S和半径参数α决定的且唯一。它的原理如图所示。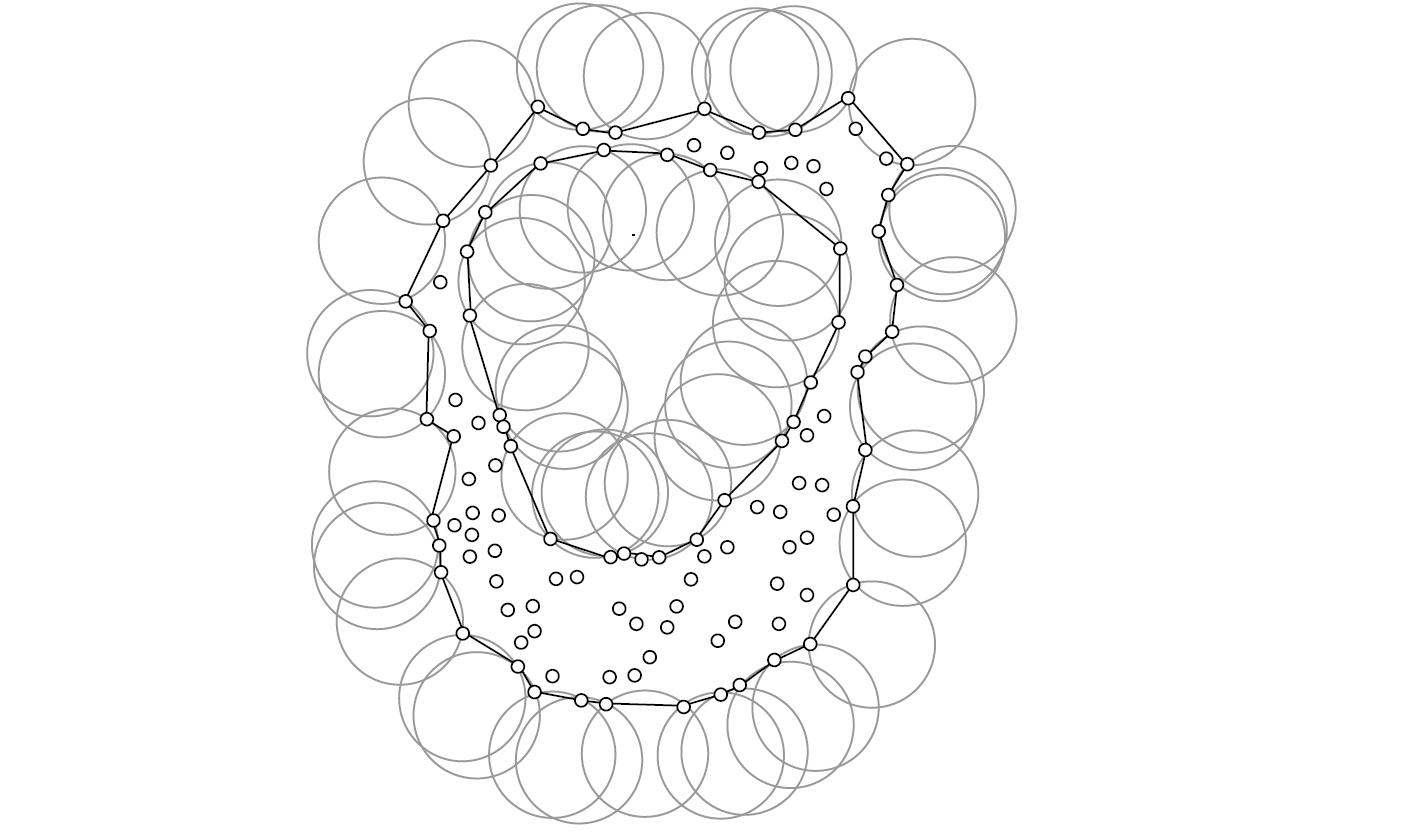

可以想象成一个半径为α的圆在点集S外滚动，当α足够大时，这个圆就不会滚到点集内部，其滚动的痕迹就是这个点集的边界线。因此，当α值很小，则每个点都是边界；如果α很大（α→∞）时，则求出的边界线为点集S的凸包。可用下式表示： \[ lim_{α→0}S_{α}=S and lim_{α→∞}S_{α}=convS \] Introduction to Alpha Shapes - Computer graphics.jpg

Alpha Shapes算法实现方法

一个有限离散点集S由n个点构成，这n个点可以组成n×(n−1)条线段，那么判断哪些线段是边界线上的线段通过以下方法进行：

在点集S内，过任意两点P1、P2绘制半径为α的圆，如果这个圆内没有其他点，则认为点P1、P2是边界点，其连线P1、P2是边界线段。假设已知两点P1、P2坐标分别是x1、y1，x2、y2，求过这两点的圆的圆心P3，实际上就是求与这两点距离为α的点P3的坐标x3、y3。获得圆心后，要判断圆内是否有其他点，则只需判断是否存在其他点到圆心的距离小于α值。

该方法需要多次的判断点是否落在园内，计算量较大。为了减少计算量，采用先建立三角网，再从三角网的外边界开始进行判断，其流程如下：

根据点集s建立Delaunay三角网；

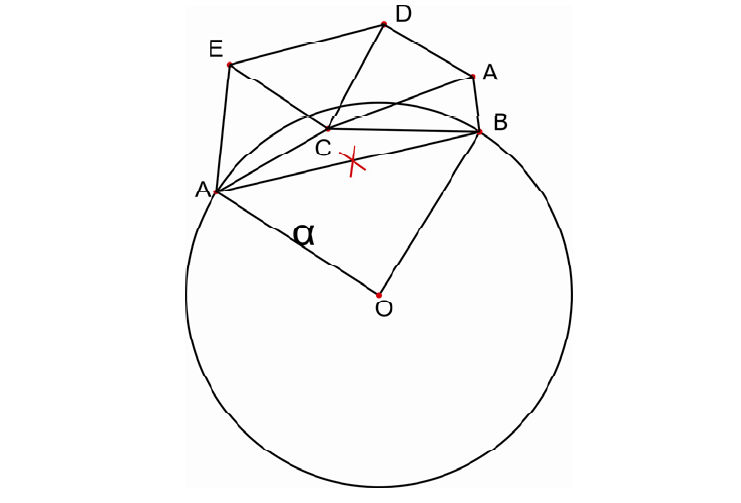
在三角网上删除不符合Alpha-Shapes要求的三角型。先删除边长大于2α的三角形；再递归判断要删除的边缘三角型，若通过三角形外边两点并且半径为α的圆包含其他点，则删除此边缘三角形。如图所示，当前所要判断的三角型为ΔABC，外边两点A和B，半径为α并且通过A，B两点的圆包含点C，则从三角网上删除ΔABC。添加新出现的边缘三角型ΔACE和ΔABC到待处理堆栈中。

在删除不符合Alpha-Shapes要求的三角型后所得到的三角网上求出三角网的边缘。该边缘即为点集s的边缘线。

Alpha Shapes算法在MATLAB中实现

MATLAB在R2014b中推出alphaShape功能函数，其语法如下：

shp = alphaShape(x,y) %使用默认alpha半径创建一个包含点 (x,y) 的二维 alpha 形状。默认 alpha 半径将生成最紧凑的拟合 alpha 形状，将所有点包括在内。
shp = alphaShape(x,y,z)
shp = alphaShape(P) %指定矩阵P的各列中的点 (x,y) 或 (x,y,z)。
shp = alphaShape(___,a) %使用上述语法中的任何参数创建一个alpha半径为a的 alpha 形状。
shp = alphaShape(___,Name,Value) %使用一个或多个Name,Value对组参数指定的其他选项。例如，您可以使用 'HoleThreshold' 隐藏内部孔或空隙。

若只是对二维或三维空间内的一组点的边界进行寻找，可以使用boundary功能函数，其语法如下：

k = boundary(x,y) %返回一个表示包围点 (x,y) 的单个相容二维边界的点索引向量。点 (x(k),y(k)) 构成边界。与凸包不同，边界可以向内部收缩以包围这些点。
k = boundary(x,y,z)
k = boundary(P) %指定矩阵 P 的各列中的点 (x,y) 或 (x,y,z)。
k = boundary(___,s) %结合上述语法指定收缩因子s。s是一个介于0和1之间的标量。将s设置为0可生成凸包，将s设置为1可生成包围这些点的紧凑边界。默认收缩因子是0.5。
[k,v] = boundary(___) %还返回一个标量 v，它是边界 k 围住的面积（二维）或体积（三维）。

下面是一个例子

%创建并绘制一个随机二维点集。
x = gallery('uniformdata',30,1,1);
y = gallery('uniformdata',30,1,10);
plot(x,y,'.')
xlim([-0.2 1.2])
ylim([-0.2 1.2])
%使用默认收缩因子计算包围这些点的边界。
k = boundary(x,y);
hold on;
plot(x(k),y(k));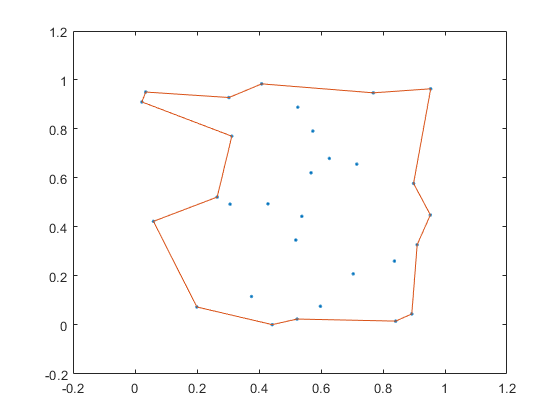

参考文献

截面最短连通路径法的散点轮廓曲面拟合离散点云原始形状及边界曲线提取算法基于路径形态学的图像边缘连接方法封闭离散点的曲线拟合方法离散点最小（凸）包围边界查找散点轮廓算法——Alpha Shapes 利用Alpha Shapes算法提取离散点轮廓线平面离散点集的边界搜索算法依据二维和三维中的点构建的多边形和多面体区域边界的类型二维或三维空间内的一组点的边界凸包